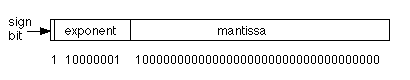Computers use binary and store values using bits, so our little system of using decimal notation is not entirely realistic. The mantissa is of course stored as a base-2 integer. The decimal point is only implied, never stored. The sign bit is stored, usually negative numbers are 1 while positive numbers have a 0 in that place. The exponent is also a base-2 integer, but excess notation is most often used.

Normalized binary mantissas would always have a 1 in the first digit of the mantissa. Fig. 21.7.1 shows a floating point number using a fictitious but nearly realistic system. Let's figure out what number is represented. First, the sign bit is 1, so the number is negative. There are 8 exponent bits, and the bit pattern in 10000001, which is 129. Usually excess notation is used, as mentioned above, and we assume that excess 128 is used in this case. Thus, the exponent is +1. However, the base of the exponent is usually not 10, but 2, so this is 21. Finally, the mantissa is 0.100000000000002 which is actually one half, or 0.5. This is because the first place to the right of the binary point would be 2^-1 which is 1/2 or 0.5. Thus, the entire number is 0.5×2¹ or 1.