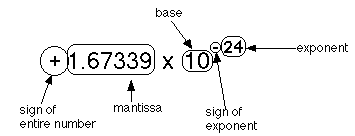
Fig. 21.1.1: Mass of Hydrogen atom showing the four parts of a real number
People need to represent real numbers in computers. Numbers which are not integers, i.e. contain fractional parts, as well as extremely large and extremely small numbers are needed by scientific and business applications, and even by people who just want to keep track of their money or balance their checkbook or convert from metric to English measurements. Floating point numbers are the computer entities which satisfy these needs and approximate real numbers.
Scientists needed to represent very large and very small numbers long before computers came along. For example, the mass of the hydrogen atom is about 1.67339×10-24 grams. This number would be 0.00000000000000000000000167339 if written out as a pure fraction, which is ridiculously clumsy to write, read, and work with.
Floating point numbers, as well as numbers in scientific notation, consist of four parts:
The base of the exponent is always fixed. Scientific notation uses 10 as the base. The mantissa in scientific notation is a real number between 1.0 and 10.0, not including 10.0.
In Fig. 21.1.1 the four parts of a number are shown:

Fig. 21.1.1: Mass of Hydrogen atom showing the four parts of a real number
Methods of encoding floating point numbers in a computer differ from scientific notation. In computers the base is almost always a power of 2 and the mantissa has a fixed number of digits past the decimal point (actually the "binary point" since the base is not 10). Naturally, the mantissa is encoded in binary, rather than decimal, since the computer can only store binary. The mantissa is usually a fraction between 0 and 1.0, not including 1.0, which is also different from scientific notation which goes from 1.0 up to 10.0.
The number of digits past the decimal point is called the precision of the number. In some cases, like 1/3 or 1/7, the digits repeat forever in a regular pattern. In other cases, such as with π, the digits repeat forever but there is no pattern. The only way to really handle such numbers, called irrationals, is to stop after a certain number of digits. Though some computers have programs to do rational arithmetic, being able to manipulate fractions like 1/3 or 1/7 precisely, the usual approach is to turn them into decimals and also chop them off after a certain number of places to the right of the decimal point. Obviously, the more digits we write after the decimal point, the more information we convey, but the more room we take up in the computer's memory to store this.
The speed of light is about 1.86×105 miles/second. 105 is 100000 so the speed is 186,000 miles/sec. Actually, it is about 186,252 miles/sec, but if we can only store 3 digits of mantissa, we would have to approximate it with 186,000. If we wanted to represent the number 1860, we could use 1.86×103, and our level of accuracy (the number of digits in the mantissa) would be identical to that of our speed of light value. Obviously 105 is much larger than 103, 100 times larger in fact, so the speed of light is much larger than 1860 yet both numbers have 1.86 as their mantissa.
The exponent can be negative or positive. A positive exponent results in a large absolute value, while a negative exponent results in a small absolute value. The speed of light has a large positive exponent while the mass of the hydrogen atom has a small negative exponent. The sign of the exponent is independent of the sign of the entire number.
Negative exponents do not affect the sign of the entire number, whether it is positive or not. Rather, they affect how close to 0 number is. Numbers with negative exponents are very close to 0, whether they are on the right or the left side of 0 on the real number line as shown in Fig. 21.1.2. The negative numbers are mirror images of the positives in this regard. -1.0x101 is much further away from 0, to the left, than 1.0×10-1.
Another way to visualize the effect of the effect of the sign of the exponent is to imagine moving the decimal point around. If the sign of the exponent is positive, move the decimal point to the right and add 0s at the end if needed. If the sign of the exponent is negative, move the decimal point to the left and add 0s between the decimal point and the mantissa.
For example, 1.86×105 would have the following equivalent representations:
mantissa exponent
---------------------
1.86 5
18.6 4
186.0 3
1860.0 2
18600.0 1
186000.0 0
A number with a small absolute value (negative exponent) such as 1.86×10-5 would have these representations:
mantissa exponent
---------------------
1.86 -5
0.186 -4
0.0186 -3
0.00186 -2
0.000186 -1
0.0000186 0
Numbers with negative exponents have a very small absolute value, regardless of the sign of the overall number, while those with positive exponents have very large absolute values. Thus -1.86×10100 has a huge absolute value, while -3.283×10-33 has a teeny absolute value. However, 3.283×10-33 is actually larger than -1.86×10100 because the first is positive while the second is negative.
In every computer system that represents and manipulates floating point numbers, the size of the exponent and the size of the mantissa are fixed, usually by the hardware. When great precision is needed, software packages, like the 'bc' calculator of UNIX, can be used. Of course, it is futile to try to represent some real numbers with infinite precision because it just can't be done! π is an example, so is 1/3, which is 0.33333333333333....
In the following discussion and examples, we will use only decimal numbers because they are easier to work with (at least as far as humans are concernd) But the same general principles apply in binary.