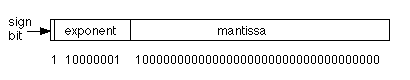
Fig. 21.7.1: Representation of 1 in a binary floating point system
Computers use binary and store values using bits, so our little system of using decimal notation is not entirely realistic. The mantissa is of course stored as a base-2 integer. The decimal point is only implied, never stored. The sign bit is stored, usually negative numbers are 1 while positive numbers have a 0 in that place. The exponent is also a base-2 integer, but excess notation is most often used.
Normalized binary mantissas would always have a 1 in the first digit of the mantissa. Fig. 21.7.1 shows a floating point number using a fictitious but nearly realistic system. Let's figure out what number is represented. First, the sign bit is 1, so the number is negative. There are 8 exponent bits, and the bit pattern in 10000001, which is 129. Usually excess notation is used, as mentioned above, and we assume that excess 128 is used in this case. Thus, the exponent is +1. However, the base of the exponent is usually not 10, but 2, so this is 21. Finally, the mantissa is 0.100000000000002 which is actually one half, or 0.5. This is because the first place to the right of the binary point would be 2-1 which is 1/2 or 0.5. Thus, the entire number is 0.5×21 or 1.
Fig. 21.7.1: Representation of 1 in a binary floating point system
A little thought reveals that if normalized numbers are always stored, then the first bit of the mantissa would always be 1. If that is so, why store it? Why not pretend it is there and use the remaining bits to store the rest of the mantissa? Indeed that is what most floating point systems do in actual computers. It allows them one more bit in the mantissa of accuracy.
So the number we would really see for +1 in our computer would look like Fig. 21.7.2:
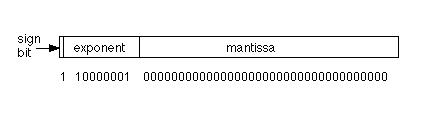
Fig. 21.7.2: Representation of 1 in binary FP with implied first bit (normalized form)
Of course this wreaks havoc with our idea of storing denormalized numbers. But not to worry. Clever hardware designers and their mathematician friends realized that if the exponent were 0, the lowest possible value, then the mantissa should represent itself exactly, without implying a leading 1. Thus, the smallest (in magnitude) normalized number would have an exponent of 00000000 and a mantissa of .10000000..... Note that the leading 1 is now .1 itself, not .11 as would be case if the exponent were 1 or larger. Then other denormalized numbers would still have an exponent of 00000000 and mantissas that were progressively smaller, with leading 0s, such as 00000000 .0100000000 and so forth. Though this makes the logic circuits more complex, it does continue to save space and improve accuracy while allowing denormalized numbers to still be represented.
One last point is that 0 is a special case. It should be 0.00000×1050 if we use our excess-50 notation, since 50-50=0. Actually, it doesn't matter what the exponent is if the mantissa is 0. However, floating point hardware reserves special bit patterns for certain error conditions. One of these is INF (infinity) which is supposed to be larger than any number. Usually, all 1s is reserved for that. Another is NaN (Not a Number) which is used to represent illegal calculations such as division by 0. Thus, the hardware usually insists on 0 using just one bit pattern and for reasons of safety and convenience this is usually all 0s. Bit patterns where the mantissa is 0 and the exponent is not are reserved for these error conditions.