Bits are organized into packets, which are just abstract divisions of the bit stream in time. A packet is a kind of data structure, like a Pascal record or a C struct. It is broken into logical units, each of which has a predefined length and a set meaning. Fig. 23.3.1 shows a typical packet format.
This packet format has fixed and variable fields. The first 40 bits, called the header, are fixed in length and meaning. The next group of bits, representing the actual data, is variable in length, although it must always be units of 8 since we are transmitting bytes. This isn't always necessary and some protocols are bit-oriented rather than byte-oriented, being able to transmit arbitrary bit streams rather than forcing them to be broken into 8-bit bytes. In order to detect how long this section is, the fixed field immediately before it, which is a 16-bit byte count, must exist and tell how many bytes will follow. 216 is 65,536, so this many bytes can be sent in one packet. Though the data field is variable in length, there is nothing non-deterministic in this packet layout. By reading the first 40 bits the receiver knows exactly what the rest of the packet will look like as it arrives over the wire.
There may be zero or several fields that follow the actual data. These comprise the trailer. In Fig. 23.3.1, the trailer consists of one field that contains a checksum which allows the receiver to determine that the packet was not altered in transmission. Error detecting and error correcting codes used in these checksums form a fascinating subfield of networking and are supported by well-known mathematical theory. We can but mention a few highlights.
The simplest form of error detecting code is parity, which adds a 1 or a 0 in order to make the number of 1s either even or odd, depending upon whether even parity or odd parity is desired. Parity can detect single errors, i.e. occurrences of a single bit in a packet being changed from 1 to 0 or 0 to 1, but it cannot fix such an error. Nor can it detect a double bit error, although it can detect a triple or any odd-numbered error. Thus parity is quite limited.
Two-dimensional parity, as discussed in the exercise, makes it possible to detect and correct single bit errors, but two-bit errors and burst errors (a sequence of bits that have all been altered or some of which have been altered) are still undetected. Fig. 23.3.2 shows a 2-dimensional parity scheme using even parity. A single bit error is detected at the intersection of a row and a column that has an incorrect parity bit.
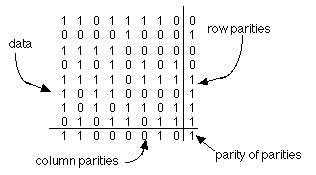
Fig. 23.3.2: 2-dimensional even parity is able to detect and fix single errors
Of course the bits really aren't transmitted in a two-dimensional form. Several methods of actually sequencing the bits onto the wire are possible -- either transmit each column at a time or each row at a time.
One method that is used by some simple protocols is a modulo sum. The ASCII bytes that come across the wire are treated as unsigned 8-bit binary numbers and added into an ongoing sum. Any carry is thrown away, which is identical to taking the 256 modulus of the sum. In fact, this may have been the origin of the term checksum, which combines the purpose (to check for errors) with the method (summing the bytes). A variation of this method used by the TCP protocol is to use the XOR function instead of full binary addition, since XOR is faster.
Checksumming by simple addition or XORing suffers from several weaknesses in that it can fail to detect some kinds of errors. For example, swapping the order of the bytes has no effect on the checksum, since addition and XOR is commutative. Mathematicians study all the various techniques and chart the characteristics of each method, such as how bit errors can it detect, how many can it correct, and how far apart error bits can be in a burst error before the method will break down.
One method that is highly reliable but too complicated for us to study here is called the cyclic redundancy code, or CRC. It uses some interesting number theory involving division of polynomials to come up with the checksums and is extremely accurate. A 16-bit long CRC code can catch all single and double errors in an arbitrarily long transmission sequence, and all burst errors of length 1 through 16, and 99.997% of 17-bit error bursts and 99.998 percent of 18-bit and longer error bursts! Obviously, it is the preferred error code, but it is somewhat complicated to compute in software, which is why it is not used everywhere. Special chips have been developed which can compute it using fast hardware called shift registers.