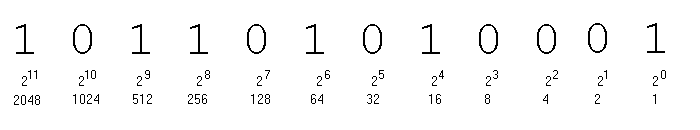
Numbers in computers are usually of two types: integers and floating point (reals.) As in mathematics, integers may be negative or positive or 0. Oftentimes only positive integers are needed and these are called unsigned integers.
Integers are encoded using base 2 or binary. This is a positional
representation system that is identical in concept to base 10 or base 8 or
base 5. Each "digit" of a numeral (this is what we call a written
representation of a number) is assigned to a place, or power of the base.
Here is a binary number written out to show its powers of 2.
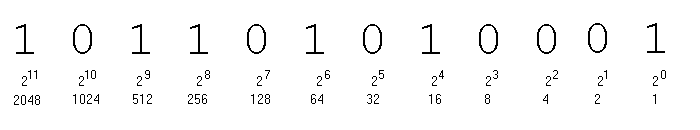
To convert from binary to decimal, just write out the powers of 2 and add up
those whose corresponding digit is 1.
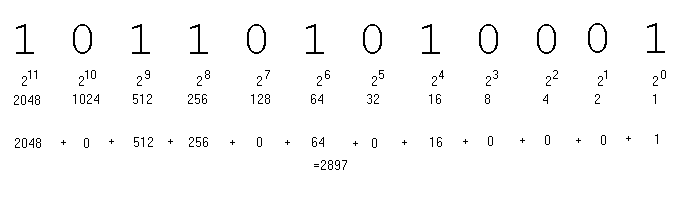
We write 1011010100012 = 289710 where the subscript indicates the base.
To convert from decimal to binary, subtract off powers of 2, and if the result is positive, write a 1. Otherwise write a 0. This method assumes that the highest power of 2 needed for this conversion is already known. Making a reasonable guess isn't hard if the powers of 2 are consulted. An alternate way, a straightforward algorithm, is to start with the 0th power of 2, 1, and subtract it. If the result is positive, guess higher. Continue this until a negative number is obtained, then back off to the previous power of 2.
Here is a table of some of the powers of 2:
n n n
n 2 n 2 n 2
------------------------------------------------------------------
0 1 11 2048 22 4,194,304
1 2 12 4096 23 8,388,608
2 4 13 8192 24 16,777,216
3 8 14 16,384 25 33,554,432
4 16 15 32,768 26 67,108,864
5 32 16 65,536 27 134,217,728
6 64 17 131,072 28 268,435,456
7 128 18 262,144 29 536,870,912
8 256 19 524,288 30 1,073,741,824
9 512 20 1,048,576 31 2,147,483,648
10 1024 21 2,097,152 32 4,294,967,296
As an example, let's convert 54000 to binary. Looking at the table, we see that 54000 lies between 32768 and 65536, so we can start at 32768. With each subtraction decision, we mark whether we could subtract with a 0 or 1, as shown below:
54000 Starting number to convert
-32768 Can subtract 32768 1
---------
21232 After subtraction
-16384 Can subtract next lower power 1
---------
4848 After subtraction
-8192 Can't subtract 0
---------
4848 Leave the number alone
-4096 Can subtract next lower power 1
---------
752 After subtraction
-2048 Can't subtract 0
---------
752 Leave the number alone
-1024 Can't subtract 0
---------
752 Leave the number alone
-512 Can subtract 512 1
---------
240 After subtraction
-256 Can't subtract 0
---------
240 Leave the number alone
-128 Can subtract 128 1
---------
112 After subtraction
-64 Can subtract 64 1
---------
48 After subtraction
-32 Can subtract 1
---------
16 After subtraction
-16 Can subtract 16 1
---------
0 After subtraction
-8 Can't subtract 0
---------
0
-4 Can't subtract 0
---------
0
-2 Can't subtract 0
---------
0
-1 Can't subtract 0
---------
0
This entire tedious process is carried out in detail as an example. The final binary numeral can be read off by lining up the 1s and 0s, starting from the top:
1101001011110000
Binary numbers might seem terribly inefficient since they seem to be a lot longer than decimal numbers. In fact, the binary equivalent of a decimal number will never be more than 3 times as long, when counting the actual digits. But computers do not see 1 and 0 the same as 4 or 5 or 7. The decimal digits would have be represented somehow using electricity, and though there are ways to do this, such as using ten different voltage levels, none are as simple or reliable as using off and on; hence the binary system.