Practice Exercise 6 Answers
-
Convert the following numbers from binary to decimal or decimal to
binary:
a.)
b.) (238 - 1) * 2 = 549,755,813,886
c.) 4638 1 0 0 1 0 0 0 0 1 1 1 1 0
- 4096 4096 2048 1024 512 256 128 64 32 16 8 4 2 1
------
542
- 512
-----
30
- 16
----
14
- 8
---
6
- 4
---
2
- 2
---
0
-
Convert the following numbers to 2's complement binary, with various
word lengths.
a.) 00000111 = 7
11111000 (flip)
+1 (add 1)
--------
11111001 = -7 in 8-bit 2's complement
b.) 10000000 = 128
01111111 (flip)
+1 (add 1)
--------
10000000 = -128 in 8-bit 2's complement
c.) 01010111 = +87 (no need to flip/add 1 since it is positive)
d.) 00000000 01010111 = 87 (in 16 bits)
11111111 10101000 (flip)
+1 (add 1)
-----------------
11111111 10101001 = -87 in 16-bit 2's complement
e.) -1 in 36 bits is 111111111111111111111111111111111111
(36 1's)
f.) -4 in 80 bits is 1111......11100
(78 1's)
-
The following numbers are encoded in 2's complement, either 8-bit or
16-bits. In each case, tell what the absolute value of the number is in
decimal.
a.) 10001010 is negative because 1st bit is 1
10001010
01110101 (flip)
+1 (add 1)
--------
01110110 = 118 so the original number was -118
b.) 1111000011110000 is negative because 1st bit is 1
1111000011110000
0000111100001111 (flip)
+1 (add 1)
----------------
0000111100010000 = 3856 so the original number as -3856
c.) 1111111111111000 is negative because 1st bit is 1
1111111111111000
0000000000000111 (flip)
+1 (add 1)
----------------
0000000000001000 = 8 so the original number as -8
d.) 0100000000000001 is positive because 1st bit is 0
^ ^
| |
16384 1 = +16385
-
Do the following arithmetic operations in 8-bit 2's complement binary.
Check your numbers with decimal arithmetic to make sure that you get the
right answer.
a.) 68 = 01000100
+ -87 = + 10101001 (2's complement, 8 bits)
------ ----------
-19 11101101 ---> 00010010 + 1 = 00010011 = -19
b.) -101 = 10011011 (details of conversion to 2's comp not shown)
+ -36 = + 11011100
------ ----------
-137 101110111 (oops, overflow, can't fit in 8 bits)
01110111 = +119, which is not -137
So when we get a carry out like (b) we have overflow and the answer
can't fit in the allotted number of bits.
-
Write all the bit patterns for 4-bits 2's complement, according to the
layout shown in Chapter 6.
bit pattern unsigned 2's complement
--------------------------------------------------------
1000 8 -8
1001 9 -7
1010 10 -6
1011 11 -5
1100 12 -4
1101 13 -3
1110 14 -2
1111 15 -1
0000 0 0
0001 1 1
0010 2 2
0011 3 3
0100 4 4
0101 5 5
0110 6 6
0111 7 7
-
Suppose you had an 8-bit computer and you did a number of additions, as
shown below. For each tell what the CNV and Z bits would be after the
operation.
a.) 10010111 C=___1__ N=___0__
+ 10001001 Z=___0__ V=___1__
-----------
1 00100000
b.) 01010111 C=___1__ N=___0__
+ 11101001 Z=___0__ V=___0__
-----------
1 01000000
c.) 00000100 C=___1__ N=___0__
+ 11111100 Z=___1__ V=___0__
-----------
1 00000000
d.) 00111011 C=___0__ N=___1__
+ 01011010 Z=___0__ V=___1__
-----------
0 10010101
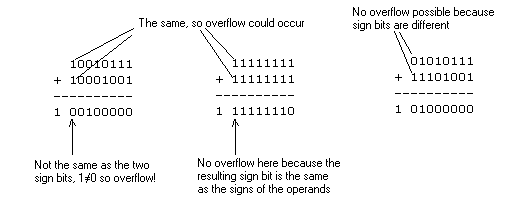
So many people get confused by the V bit, which signals 2's complement
overflow. (Remember that C signals pure overflow, or carry-out. The
C bit is identical to the leftmost bit of the answer, the one that is
slightly separated out in the answers above.)
Here are 2 ways to calculate V. First, compare the leftmost bits of the
two operands. If they are different, V is automatically 0. If they are
the same, V is 1 only if they are different from the corresponding bit
in the answer. Otherwise, if they are all the same, V=0.
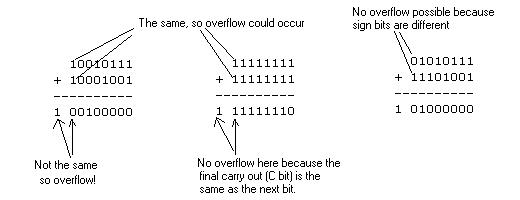
The second way is to compare the the C bit to the N bit. If C is the same
as N, then V must be 0. But if they differ, then check to see if the two
leftmost bits of the two operands are the same. If so, V=0. If not, V=1.
-
Following are some 8-bit values to which shift operations are applied.
Write down the new values after shifting.
a.) 1 0 1 1 0 1 1 1 logical shift left 1 bit (SHLL)
/ / / / / / / / /
lost 0 1 1 0 1 1 1 0 (insert 0 from outer space)
b.) 1 0 1 1 0 1 1 1 logical shift right 1 bit (SHLR)
\ \ \ \ \ \ \ \ \
0 1 0 1 1 0 1 1 lost (insert 0 from outer space on the left)
c.) 1 0 1 1 0 1 1 1 circular shift right 1 bit (SHCR)
\ \ \ \ \ \ \ \
1 1 0 1 1 0 1 1 \ (copy the rightmost 1 around to the left)
^ |
| |
+---------------+
d.) 1 0 1 1 0 1 1 1 arithmetic shift right 1 bit (SHAR)
|\ \ \ \ \ \ \ \
1 1 0 1 1 0 1 1 lost (copy the sign bit into two bits)
e.) 1 0 1 1 0 1 1 1 arithmetic shift left 1 bit (SHAL)
|/ / / / / / / /
1 1 1 0 1 1 1 0 (insert 0 from outer space)
X
problem here, 1 and 0 clash, hence overflow occurs
-
For the following pairs of operands, apply bitwise Boolean operations.
a.) 10010001111
& 01100011101 (and)
-------------
00000001101
b.) 10010001111
| 01100011101 (or)
-------------
11110011111
c.) ^ 10010001111 (not)
-------------
01101110000 (same as "flip" operation)
-
Using the ASCII character set, write some C statements. Imagine that
there is a character variable called ch, declared as char ch;
a.) determine if the character in ch is printable
if (ch >= 32 && ch <= 126) ...
b.) determine if the character in ch is a printable punctuation symbol
if (ch >= 32 && ch <= 47 || ch >= 58 && ch <= 64 ||
ch >= 91 && ch <= 96 || ch >= 123 && ch <= 126) ...
c.) convert an uppercase letter to lowercase (don't need to check to make
sure it is uppercase first)
ch += 32; 'A' = 65, 'a' = 97 97-65 = 32
-
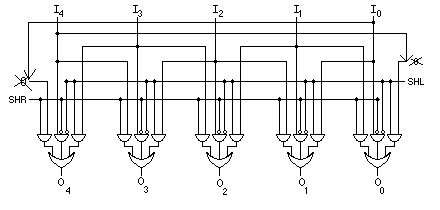
Below is the circuit for the 1-bit left and right logical shifter shown
in Fig. 2 of Chapter 6. Make modifications so that it is a circular shifter
instead. (Remember that a circular shifter does not insert 0s at the end,
but moves the end bits around.)
